

Normally when we develop programs, unavoidably want to do all sorts of transformation processing to the image. Especically the transformation bewtween multiple coordinate system.
It is not only complicated but also inefficient. We can combine multiple transformations by using transformation matrix and matrix multiplication. Finally, we can get the desired result by using a matrix for each point.
Important Note: The order of Transformation does affect the result. In most cases, The order of Matrix Transformation is Scale -> Rotate -> Translate.

Before, we only considered 3D vertices as a (x,y,z) triplet. For making the 3D transformation easier, We will now have (x,y,z,w) vectors.
If w == 1, then the vector (x,y,z,1) is a position in space. If w == 0, then the vector (x,y,z,0) is a direction.
A classic example of homogeneous coordinates is to make the translation of a vector become linear transformation.
Translation without Homogeneous Coordinates
\begin{equation} \begin{bmatrix} x’ \
y’ \
z’ \
\end{bmatrix} = \begin{bmatrix} t_x \
t_y \
t_z \
\end{bmatrix} + \begin{bmatrix} x \
y \
z \
\end{bmatrix} \end{equation}
Translation in Homogeneous Coordinates
\begin{equation} \begin{bmatrix} x’ \
y’ \
z’ \
1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & t_x \
0 & 1 & 0 & t_y \
0 & 0 & 1 & t_z \
0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \
y \
z \
1 \end{bmatrix} \end{equation}
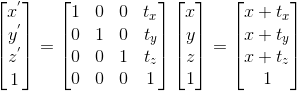
A change from one location to another is represented by a translation matrix, T. This matrix translates an entity by a vector $t = (tx, ty, tz)$. $T$ is given below by

Note: The square on the left is transformed with a translation matrix T(5, 2, 0), whereby the square is moved 5 distance units to the right and 2 upward.
Code Example: Translate (3, -2, 1.5) from a start point (2, 3, 5)
public Matrix4x4 matrix;
public Vector4 vector;
void Start()
{
// if the w is 1 represent a point, 0 represent a vector
vector = new Vector4(transform.position.x, transform.position.y, transform.position.z, 1);
matrix = Matrix4x4.identity;
Debug.Log("Before Translate: " + transform.localToWorldMatrix);
matrix.m03 = 3; // move (3,-2,1.5)
matrix.m13 = -2;
matrix.m23 = 1.5f;
// Translate
vector = matrix * vector;
transform.position = new Vector3(vector.x, vector.y, vector.z);
Debug.Log("After Translate: " + transform.localToWorldMatrix);
}
Output:
Before Translate:
1.00000 0.00000 0.00000 2.00000
0.00000 1.00000 0.00000 3.00000
0.00000 0.00000 1.00000 5.00000
0.00000 0.00000 0.00000 1.00000
After Translate:
1.00000 0.00000 0.00000 5.00000
0.00000 1.00000 0.00000 1.00000
0.00000 0.00000 1.00000 6.50000
0.00000 0.00000 0.00000 1.00000
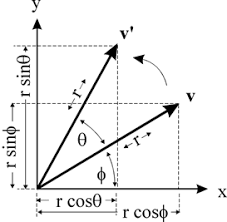
In two dimensions, the rotation matrix is simple to derive. Assume that we have a vector, $v = (v_x, v_y)$, which we parameterize as $v = (v_x, v_y) = (r cos \theta, r sin \theta)$. If we were to rotate that vector by $\phi$ radians (counterclockwise), then we would get $u = (r cos(\theta + \phi), r sin(\theta + \phi))$. This can be rewritten as
\begin{equation} u = \begin{bmatrix} rcos(\theta+\phi) \
rsin(\theta+\phi) \end{bmatrix} = \begin{bmatrix} r(cos\theta cos\phi - sin\theta sin\phi) \
r(sin\theta cos\phi + cos\theta sin\phi) \end{bmatrix} = \begin{bmatrix} cos\phi & -sin\phi \
sin\phi & cos\phi \end{bmatrix} \begin{bmatrix} r cos\theta \
r sin\theta \end{bmatrix} = R(\phi)v \end{equation}
(1) Rotate Along X-Axis:
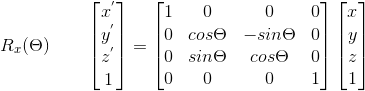
(2) Rotate Along Z-Axis:
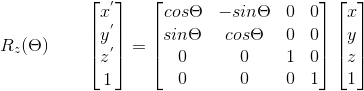
(3) Rotate Along Y-Axis:

Above Described the roation in matrix. rotating along the X and Y axis are similar, but Y is not. The reason is that based on the right hand rule, rotating along the y-axis has a different axial order. When you point the right hand thumb in the axis you want to rotate along with, we can see the order of axis based on the right hand rule. (seec image below)
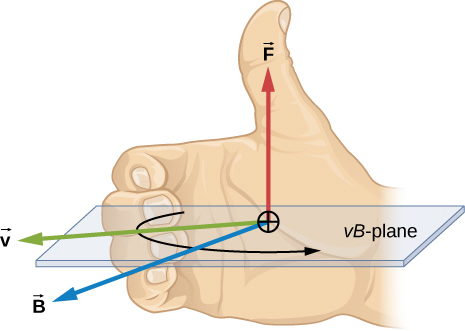
Code Example: Rotate along respectively x, y, z 30 degree
Matrix4x4 matrix;
Vector4 vector;
public float angle = 30;
public enum Axis { X, Y, Z }
public Axis axis;
void Start()
{
matrix = Matrix4x4.identity;
Debug.Log("Before Rotate: " + matrix);
switch (axis)
{
case Axis.X:
matrix.m11 = Mathf.Cos(angle * Mathf.Deg2Rad);
matrix.m12 = -Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m21 = Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m22 = Mathf.Cos(angle * Mathf.Deg2Rad);
Debug.Log("After Rotate(along x-axis) : " + matrix);
break;
case Axis.Y:
matrix.m01 = Mathf.Cos(angle * Mathf.Deg2Rad);
matrix.m02 = Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m21 = -Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m22 = Mathf.Cos(angle * Mathf.Deg2Rad);
Debug.Log("After Rotate(along y-axis): " + matrix);
break;
case Axis.Z:
matrix.m01 = Mathf.Cos(angle * Mathf.Deg2Rad);
matrix.m02 = -Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m11 = Mathf.Sin(angle * Mathf.Deg2Rad);
matrix.m12 = Mathf.Cos(angle * Mathf.Deg2Rad);
Debug.Log("After Rotate(along z-axis): " + matrix);
break;
}
transform.rotation = MatrixToQuaternion(matrix);
}
Quaternion MatrixToQuaternion(Matrix4x4 _matrix)
{
float qw = Mathf.Sqrt(1f + _matrix.m00 + _matrix.m11 + _matrix.m22) / 2;
float w = 4 * qw;
float qx = (_matrix.m21 - _matrix.m12) / w;
float qy = (_matrix.m02 - _matrix.m20) / w;
float qz = (_matrix.m10 - _matrix.m01) / w;
return new Quaternion(qx, qy, qz, qw);
}
Output:
Before Rotate:
1.00000 0.00000 0.00000 0.00000
0.00000 1.00000 0.00000 0.00000
0.00000 0.00000 1.00000 0.00000
0.00000 0.00000 0.00000 1.00000
After Rotate(along x-axis):
1.00000 0.00000 0.00000 0.00000
0.00000 0.86603 -0.50000 0.00000
0.00000 0.50000 0.86603 0.00000
0.00000 0.00000 0.00000 1.00000
After Rotate(along y-axis):
1.00000 0.86603 0.50000 0.00000
0.00000 1.00000 0.00000 0.00000
0.00000 -0.50000 0.86603 0.00000
0.00000 0.00000 0.00000 1.00000
After Rotate(along z-axis):
1.00000 0.86603 -0.50000 0.00000
0.00000 0.50000 0.86603 0.00000
0.00000 0.00000 1.00000 0.00000
0.00000 0.00000 0.00000 1.00000
\begin{equation} R_{Arbitrary} = \begin{bmatrix} n_x^2(1 - \cos \theta) + \cos \theta & n_x n_y ( 1 - \cos \theta ) -n_z \sin \theta & n_x n_z ( 1 - \cos \theta ) + n_y \sin \theta \\ n_xn_y(1 - \cos \theta) + n_z \sin \theta & n_y^2(1 - \cos \theta) + \cos \theta & n_yn_z(1 - \cos \theta) - n_x \sin \theta \
n_xn_z(1 - \cos \theta) - n_y \sin \theta & n_yn_z(1 - \cos \theta) + n_x \sin \theta & n_z^2(1 - \cos \theta) + \cos \theta\
\end{bmatrix} \end{equation}
So Let prove this complex matrix:
For rotating about an arbitrary axis, we firstly consider $v$ is a vector in 3D space, we need to get $v^\prime$ which is a vector that obtained by rotating $v$ along $n$ axis $\theta$ angle. (n is a unit vector )
Step 1: Get the projection of $v$ on $n$, denoted as ${proj_n}v$.
\[{proj_n}v = \frac{v\cdot n}{\|n\|^2} n\]| Because n is a unit vector, so its magnitude $ | n|$ is 1. We can simplify ${proj_n}v$ to |
Step 2: Get the vector $v_\perp$ which is a vector from \overrightarrow{v} that perpendicular to ${proj_n}v$.
\[v_\perp = v- {proj_n}v = v - (v\cdot n)n\]Step 3: Get the $w$ which is the cross product of $n$ and $v_\perp$. Based on the definition of cross product $w$ is a vector that perpendicular to a plane fixed by $n$ and $v_\perp$. Also $n$ is a unit vector, and n also perpendicular to $v_\perp$, so the length between w and $v_\perp$ are same.
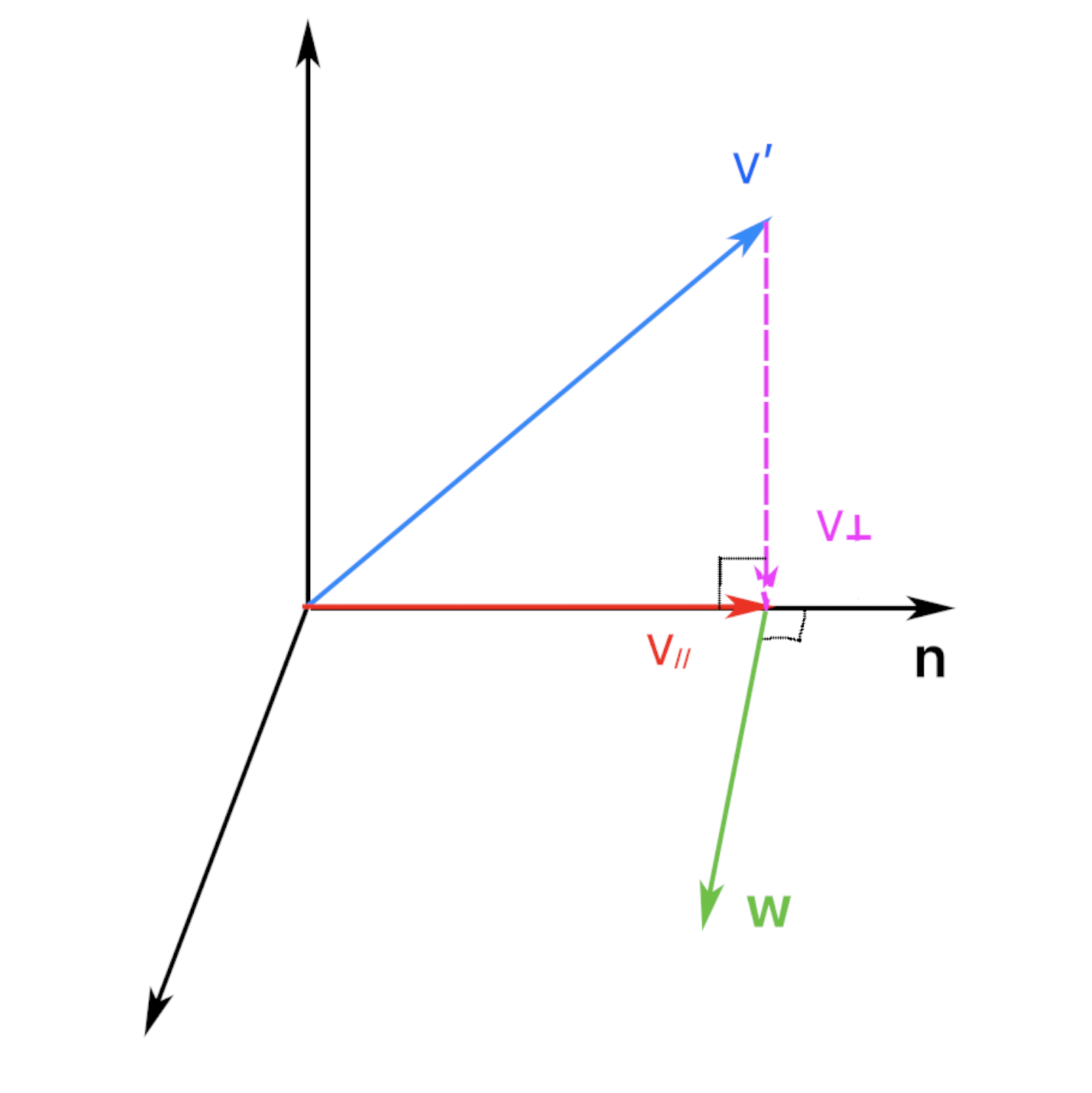
Step 4: Get $v_\perp^\prime$ which is a vector that obtained by rotating $v_\perp$ along $n$ axis $\theta$ angle.
\begin{align} v_\perp^\prime &= v_\perp \cos \theta + w\sin \theta \\ &= \left[ v - \left( v^Tn \right)n \right] \cos \theta + \left( n \times v \right) \sin \theta \end{align}
Besed on $v_\perp^\prime$, can get $v^\prime$
\begin{align} v^\prime &= v_\perp^\prime + v_\parallel \\ &= \left[ v - \left( v^Tn \right)n \right] \cos \theta + \left( n \times v \right) \sin \theta + (v^Tn)n \end{align}
Step 5: substituting $v = \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix}$, $v = \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}$ $v = \begin{bmatrix} 0 \\ 0 \\ 1 \end{bmatrix}$ into above equation.
\begin{align}
v^\prime_x &= \left( \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} - \left( \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \left( \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \times \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \right) \sin \theta + \left( \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &=\left( \begin{bmatrix} 1 \\ 0 \\ 0 \\ \end{bmatrix} - n_x \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \begin{bmatrix} 0 \\ n_z \\ -n_y \\ \end{bmatrix} \sin \theta + n_x \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &= \begin{bmatrix} 1 - n_x^2 \\ -n_x n_y \\ -n_x n_z \\ \end{bmatrix} \cos \theta + \begin{bmatrix} 0 \\ n_z \\ -n_y \\ \end{bmatrix} \sin \theta + \begin{bmatrix} n_x^2 \\ n_x n_y \\ n_x n_z \\ \end{bmatrix} \\ &= \begin{bmatrix} \cos \theta - n_x^2 \cos \theta + n_x^2 \\ -n_xn_y \cos \theta + n_z \sin \theta + n_xn_y \\ -n_xn_z \cos \theta - n_y \sin \theta + n_xn_z \end{bmatrix} \\ &= \begin{bmatrix} n_x^2(1 - \cos \theta) + \cos \theta \\ n_xn_y(1 - \cos \theta) + n_z \sin \theta \\ n_xn_z(1 - \cos \theta) - n_y \sin \theta \end{bmatrix} \end{align}
\begin{align} v^\prime_y &= \left( \begin{bmatrix} 0 \\ 1 \\ 0\\ \end{bmatrix} - \left( \begin{bmatrix} 0 \\ 1 \\ 0\\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \left( \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \times \begin{bmatrix} 0\\ 1\\ 0\\ \end{bmatrix} \right) \sin \theta + \left( \begin{bmatrix} 0 \\ 1 \\ 0\\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &=\left( \begin{bmatrix} 0 \\ 1 \\ 0 \\ \end{bmatrix} - n_y\begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \begin{bmatrix} -n_z \\ 0 \\ n_x \\ \end{bmatrix} \sin \theta + n_y \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &= \begin{bmatrix} - n_x n_y \\ 1 - n_y^2 \\ -n_y n_z \\ \end{bmatrix} \cos \theta + \begin{bmatrix} -n_z\\ 0 \\ n_x \\ \end{bmatrix} \sin \theta + \begin{bmatrix} n_x n_y \\ n_y^2 \\ n_y n_z \\ \end{bmatrix} \\ &= \begin{bmatrix} -n_x n_y \cos \theta -n_z \sin \theta + n_x n_y \\ \cos \theta -n_y^2 \cos \theta + n_y^2 \\ -n_yn_z \cos \theta + n_x \sin \theta + n_yn_z \end{bmatrix} \\ &= \begin{bmatrix} n_x n_y ( 1 - \cos \theta ) -n_z \sin \theta \\ n_y^2(1 - \cos \theta) + \cos \theta \\ n_yn_z(1 - \cos \theta) + n_x \sin \theta \end{bmatrix} \end{align}
\begin{align} v^\prime_z &= \left( \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} - \left( \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \left( \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \times \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \right) \sin \theta + \left( \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} \cdot \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &=\left( \begin{bmatrix} 0 \\ 0 \\ 1 \\ \end{bmatrix} - n_z\begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \right) \cos \theta + \begin{bmatrix} n_y \\ -n_x \\ 0 \\ \end{bmatrix} \sin \theta + n_z \begin{bmatrix} n_x \\ n_y \\ n_z \\ \end{bmatrix} \\ &= \begin{bmatrix} - n_x n_z \\ -n_y n_z \\ 1 - n_z^2 \\ \end{bmatrix} \cos \theta + \begin{bmatrix} n_y \\ -n_x \\ 0 \\ \end{bmatrix} \sin \theta + \begin{bmatrix} n_x n_z \\ n_y n_z \\ n_z^2 \\ \end{bmatrix} \\ &= \begin{bmatrix} -n_x n_z \cos \theta +n_y \sin \theta + n_x n_z \\ -n_yn_z \cos \theta - n_x \sin \theta + n_yn_z \\ (1 - n_z^2) \cos \theta + n_z^2 \end{bmatrix} \\ &= \begin{bmatrix} n_x n_z ( 1 - \cos \theta ) + n_y \sin \theta \\ n_yn_z(1 - \cos \theta) - n_x \sin \theta \\ n_z^2(1 - \cos \theta) + \cos \theta \end{bmatrix} \end{align}
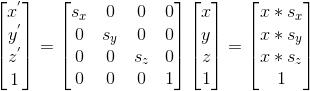
eg: scale (1.5, 2, 3) from the atart scale (1, 1, 1)
public Matrix4x4 matrix;
public Vector4 vector;
void Start()
{
Debug.Log("Before scale: " + transform.localToWorldMatrix);
matrix = Matrix4x4.identity;
// if the w is 1 represent a point, 0 represent a vector
vector = new Vector4(transform.localScale.x, transform.localScale.y, transform.localScale.z, 1);
//scale times
matrix.m00 = 1.5f; // scale x
matrix.m11 = 2; // scale y
matrix.m22 = 3; // scale z
vector = matrix * vector;
transform.localScale = new Vector3(vector.x, vector.y, vector.z);
Debug.Log("After scale: " + transform.localToWorldMatrix);
}
Output:
Before scale:
1.00000 0.00000 0.00000 2.00000
0.00000 1.00000 0.00000 3.00000
0.00000 0.00000 1.00000 5.00000
0.00000 0.00000 0.00000 1.00000
After scale:
1.50000 0.00000 0.00000 2.00000
0.00000 2.00000 0.00000 3.00000
0.00000 0.00000 3.00000 5.00000
0.00000 0.00000 0.00000 1.00000
Scale Transformation has two types of scale operation, Uniform Scaling and Non-Uniform Scaling.
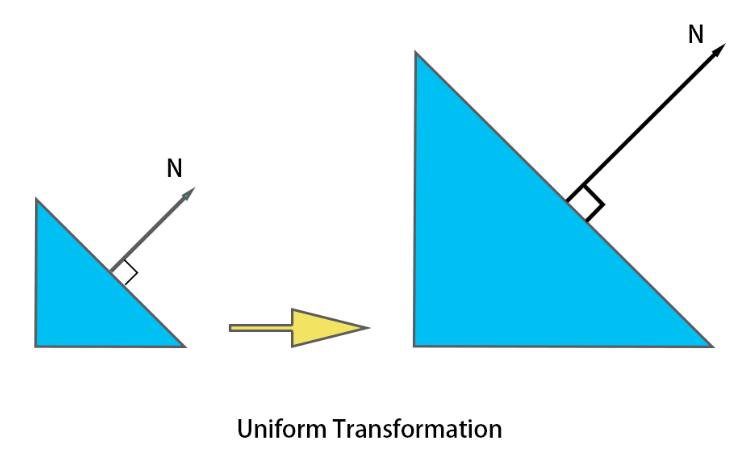
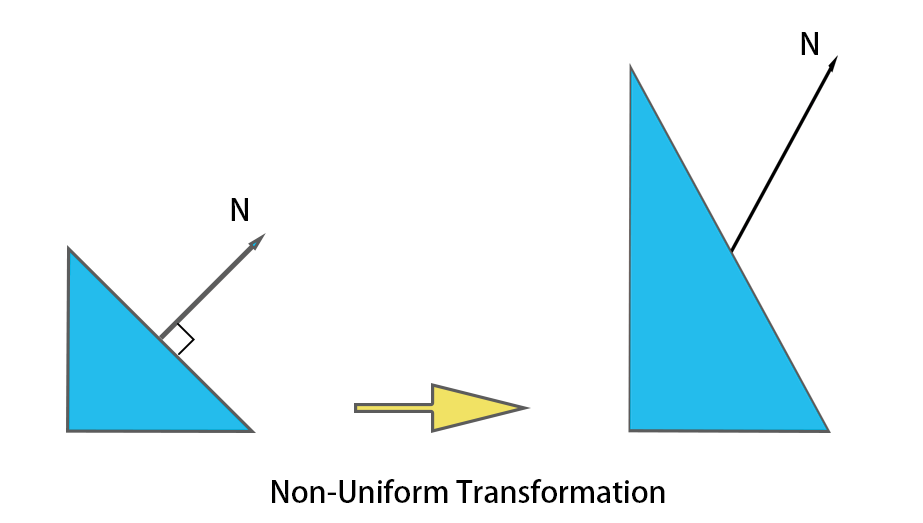
From above image, we can see Non- Uniform Transformation will cause the object normal not be perpendicular to the surface, we have to do Normal Transformation to fix this issue. In the rendering pipeline, the coordinates of the model are transformed from local space to world space via the Model matrix (M). The Normal Transformation matrix is the transposition matrix for the inverse matrix of the vertex position transformation matrix, which is $(M^-1)^T$
For the derivation method, refer to the this Link
End –Cheng Gu