Cross Or Dot

The Cross Product and the Dot Product are the most common calculations of Vector. In the Game Development, it is necessary to understand both of them. The biggest difference between them is that:

The result of dot product is a value The result of cross product is a vector

1. Dot Product

The dot product of two n-dimensional vectors A and B, written as A ⋅ B, it can calculate the length of the projection:

eg:

if:
\(\large \qquad Vector3\:\: v_1 = (x_1,y_1,z_1), Vector3\:\: v_2 = (x_2,y_2,z_2)\)

then:
\(\large \qquad v_1 \cdot v_2 = {x_1}{x_2}+{y_1}{y_2}+{z_1}{z_2}\)

Follow the law of trig it can write as:
\(\large \qquad A\cdot B = \|A\|\|B\| cos\theta\)

Follow up, it also can write as:
\(\large\qquad\theta = acos (\frac{A\cdot B}{\|A\|\|B\| })\)

Dot Product also can calculate the projection of a vector by giving A and B vectors. Basic trigonometry tells us that the length of the side adjacent to $\theta$ is given by \(\|B\| cos\theta\). Shown as below image:

The length of the projection of the Vector A onto the Vector B is given by \(\large\frac{A⋅B}{\|B\|}\), because \(A⋅B = \|A\| \|B\| cos\theta\).

Therefore, in order to get the Vector of with this length, we can just multiply by the unit vector of B, which is \(\Large\frac{B}{\|B\|}\), we can get the following formula:

The position relation of two vectors can be determined by the sign of the dot product of these two vector.

1. If the dot product = 0, these two vectors are perpendicular.
2. If the dot product <0, the angle between two Vector is 90 ~ 180. Two Vector point mostly opposite direction.
3. If the dot product >0, the angle between two Vector is 0 ~ 90. Two Vector point mostly same direction.

The dot product A ⋅ B may also be expressed as the matrix product

\begin{equation} A_T B = \begin{bmatrix}A_1 & A_2 & \cdots & A_n\end{bmatrix} \begin{bmatrix}B_1 \\ B_2 \\ \vdots \\ B_n\end{bmatrix} \end{equation}

Example in Game Development:

(1) Get the Angle of two vectors: range [0, 180], whether the view of the game monster can be viewed to the player, and can be used to calculate whether the enemy is within the range of the character’s attack.

Vector A,B;
float dotValue = Vector3.Dot (A.normalized, B.normalized);
float angle = Mathf.Acos(dotValue) * Mathf.Rad2Deg;  
//However. there is a easier way to do it in unity by using Vector.Angle().
//float angle= Vector3.Angle (Vector3 from, Vector3 to) 

(2) Determine if the target is in front of you, or behind you.

 Vector3 dirToTarget = (model.target.transform.position - model.character.transform.position).normalized;
float dotValue=Vector3.Dot(dirToTarget, transform.forward)
if(dotValue>0)
{
    print("Target is in front of you");
}else if(dotValue<0)
{
    print("Target is behind you");
}else{
    print("Target is on the left or right.");
}

(3) Simulate the flight status of the aircraft

float dotValue = Vector3.Dot(transform.forward, Vector3.up);
if (dotValue < 0)
{
    print("This plane is flying down");
}
else if (dotValue > 0)
{
    print("This plane is flying up");
}
else
{
    print("This plane is flying in parallel ");
}

2. Cross Product

The cross product of two three-dimensional vectors, returns a new vector that is perpendicular to both of the vectors being multiplied together. This property has many uses in computer graphics, one of which is a method for calculating a surface normal at a particular point given two distinct tangent vectors.

The cross product of two 3D vectors A and B, written as A × B, is a vector quantity given by the formula:

This equation seems no regularity, but it has, shown as below:

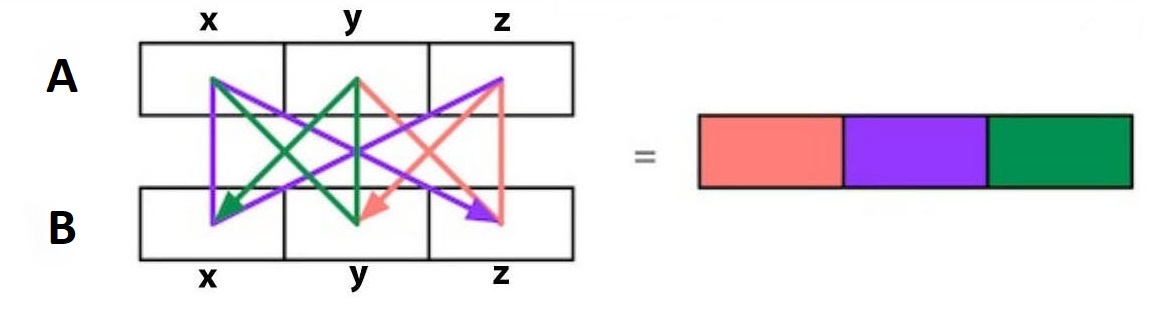
Follow the law of trig it can write as:
\(\large \qquad \|A×B\|=\|A\|\|B\|sin\theta\)

Follow up, it also can write as:
\(\large \qquad \theta = asin (\frac{\|A×B\|}{\|A\|\|B\| })\)

The cross product of two vectors, the result of the cross product is a vector instead of a value. Also, the cross product of two vectors is perpendicular to the coordinate plane of these two vectors.

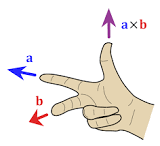
In Math, it satisfy right hand rule, a x b = -b x a. So we can use the result of Cross product’s value is positive or negative to determine a and b’s relative position.

`Right-hand Cooridinate System`

`Left-hand Cooridinate System`

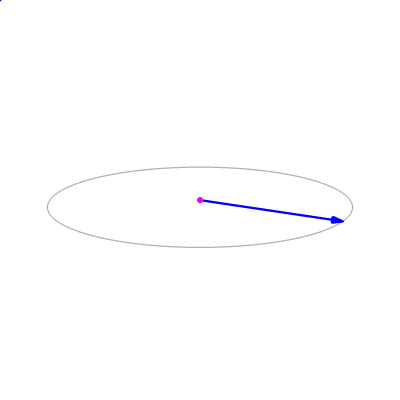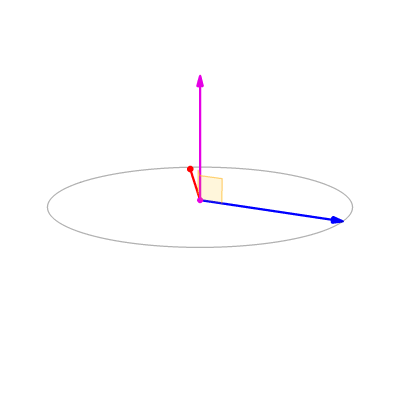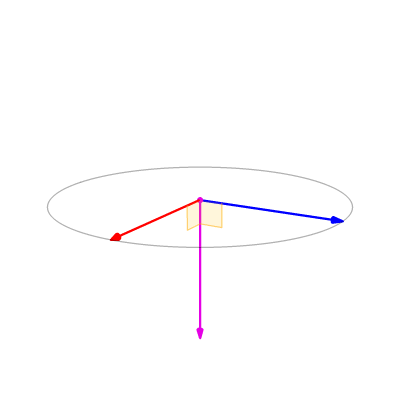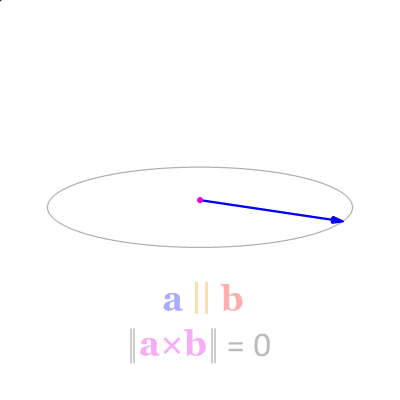
`Normal vector of a plane is the Cross Product of the coordinate plane of x and y vectors.`

Example in Game Development:

(1) WallWalking:

> The core is to use cross product cauculate the normal of wall's plane, and ground plane's normal to implement into player's Up direction

(2) Determine the target is on your right or left:

> if return a negative value, the target is on the left,
if return a positive value, the target is on the right,
if return 0, the the target is on the front side or back side

Vector3.Cross(transform.forward, target.position).y

(3) Get the area size of a parallelogram which formed by 2 objects

S = |b| * |a| * sin(θ)

(4) Get the angle between two vectors

Vector3 a, b;
float value = Vector3.Cross(a.normalized, b.normalized);
float angle = Mathf.Asin(value) * Mathf.Rad2Deg;

(5) Can Determine if two vector is Parallel or Intersecting.

In conclusion, Dot Product determine the angle of two Vectors, Cross Product determine the direction of two Vectors.

For instance, when an enemy behind you, Cross Product determine whether you should turn left or turn right to face to the enemy quickly; the Dot Product can get the angle size you need to turn towards the enemy.

End –Cheng Gu