

Convolution is very useful in many areas, one of the most common application is the image processing.
In image processing, there is a basic processing method: linear filtering. The image to be processed can be think as a large matrix, and each pixel of the image corresponds to each element of the matrix. For example, assuming that the resolution of our plane is 1024 * 768, then the corresponding large matrix’s number of rows = 1024, the number of columns = 768.
What is used for filtering is a small filter matrix known as convolution kernel, and the filter matrix is a square matrix (such as 2X2, 3x3, 4x4).
Filtering is to calculate the product of the pixels around it and the corresponding position elements of the filter matrix(kernel) for each pixel in the large matrix, and then add the results together to get the final value as the value of this pixel. Convolution need to filter each pixel in the image.
Below is the schematic diagram of image convolution calculation:
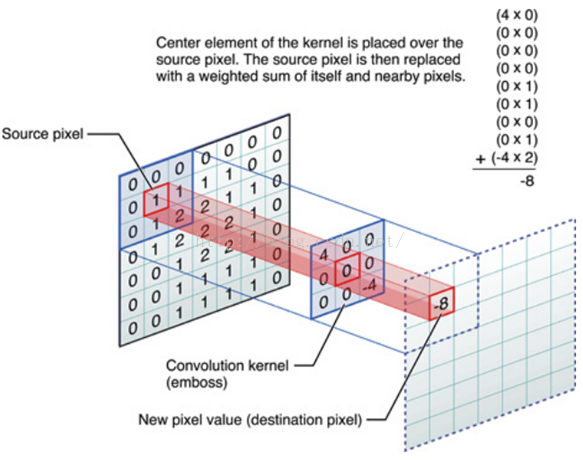
The operation of multiplying and summing the corresponding elements of the image (large matrix) and the small filter matrix(kernel) is called Convolution or Correlation. The only difference between these two is that the convolution needs to flip the convolution kernel before the calculation, and the correlation doesn't need to be flipped.
Sobel Operator (also called Sobel Filtering), is a two 3x3 matrix that is mainly used to calculate the gradient of a point in the image in the horizontal/vertical direction.
Sobel Operator has two filter matrix(kernel): Gx and Gy. Gx is used to calculate horizontal gradient, Gy is used to calculate vertical gradient.
\begin{equation} G_x = \begin{bmatrix} -1 & 0 & +1 \
-2 & 0 & +2 \
-1 & 0 & +1 \end{bmatrix} G_y = \begin{bmatrix} -1 & -2 & -1 \
0 & 0 & 0 \
+1 & +2 & +1 \end{bmatrix} \end{equation}
Note: the two gradient matrices listed here correspond to the horizontal axis from left to right and the vertical axis from top to bottom, which looks like this:
It can be used to detect the edge of an image, or to calculate the normal vector of a pixel point.
Suppose the pixels around a pixel of the image to be processed are as follows:
\begin{equation} \begin{bmatrix} up left & up & up right \
left & center & right \
down left & down & down rights \end{bmatrix} \end{equation}
Then:
new value of horizontal pixel = \((-1)*up left + (-2)*left + (-1)*down left + 1*up right + 2*right + 1*down right\)
new value of vertical pixel = \((-1)*up left + (-2)*up + (-1)*up right + 1*down left + 2*down + 1*down right\)
Note: Normally when we are doing image convolution, we need to
flipto convolutionkernel, but Sobel operator will get thesame resultafter flipping the convolution, so we don’t have to flip it when using Sobel Operator.
\begin{equation} Original Kernel = \begin{bmatrix} a & b & c \
d & e & f \
g & h & i \end{bmatrix} \end{equation}
\begin{equation} Flipped Kernel = \begin{bmatrix} i & h & g \
f & e & d \
c & b & a \end{bmatrix} \end{equation}

End –Cheng Gu