

| Usage | Attribute | ||
|---|---|---|---|
| Add items to Unity’s menus | MenuItem, AddComponentMenu, ContextMenu, ContextMenuItem, CreateAssetMenu | ||
| Show or hide information | Header, HelpURL, Tooltip, HideInInspector | ||
| Layout display in Inspector | Multiline, Range, Space, TextArea | ||
| Define constraints for component usage | RequireComponent, DisallowMultipleComponent | ||
| Specify whether to remember the value of a field or not | NonSerialized, Serializable | ||
| Execute callback functions even when Editor isn’t in playmode | ExecuteInEditMode | ||
| Configure the usage of the ColorPicker | ColorUsage |
using System.Collections.Generic;
using System;
public class PriorityQueue<T> where T : IComparable<T>
{
List<T> data;
public int Count { get { return data.Count; }}
public PriorityQueue() // Constructor
{
this.data = new List<T>();
}
// Add an item to the queue and sort using a min binary heap
public void Enqueue(T item)
{
// Add the item to the end of the data List
data.Add(item);
// Start at the last position in the heap
int childindex = data.Count - 1;
// Sort using a min binary heap
while (childindex > 0)
{
// Find the parent position in the heap
int parentindex = (childindex - 1) / 2;
// If parent and child are already sorted, stop sorting
if (data[childindex].CompareTo(data[parentindex]) >= 0)
break;
// Otherwise, swap parent and child
T tmp = data[childindex];
data[childindex] = data[parentindex];
data[parentindex] = tmp;
// Move up one level in the heap and repeat until sorted
childindex = parentindex;
}
}
// Remove an item from queue and keep it sorted using a min binary heap
public T Dequeue()
{
// Get the index for the last item
int lastindex = data.Count - 1;
// Store the first item in the List in a variable
T frontItem = data[0];
// Replace the first item with the last item
data[0] = data[lastindex];
// Shorten the queue and remove the last position
data.RemoveAt(lastindex);
// Decrement our item count
lastindex--;
// Start at the beginning of the queue to sort the binary heap
int parentindex = 0;
// Sort using min binary heap
while (true)
{
// Choose the left child
int childindex = parentindex * 2 + 1;
// If there is no left child, stop sorting
if (childindex > lastindex)
break;
// The right child
int rightchild = childindex + 1;
// If the value of the right child is less than the left child, switch to the right branch of the heap
if (rightchild <= lastindex && data[rightchild].CompareTo(data[childindex]) < 0)
{
childindex = rightchild;
}
// If the parent and child are already sorted, then stop sorting
if (data[parentindex].CompareTo(data[childindex]) <= 0)
break;
// If not, then swap the parent and child
T tmp = data[parentindex];
data[parentindex] = data[childindex];
data[childindex] = tmp;
// Move down the heap onto the child's level and repeat until sorted
parentindex = childindex;
}
// Return the original first item
return frontItem;
}
// Look at the first item without dequeuing
public T Peek()
{
T frontItem = data[0];
return frontItem;
}
// Is the item contained in the data List?
public bool Contains(T item)
{
return data.Contains(item);
}
// Return the data as a generic List
public List<T> ToList()
{
return data;
}
}
// while we have not reached the goal node... (note that are missing a null reference check in the videos)
while (!isComplete && m_frontierNodes != null)
{
// if there are still open Nodes to explore...
if (m_frontierNodes.Count > 0)
{
// get the next available Node from the priority queue
Node currentNode = m_frontierNodes.Dequeue();
// mark this Node as explored
if (!m_exploredNodes.Contains(currentNode))
{
m_exploredNodes.Add(currentNode);
}
// expand the frontier based on our search mode
switch (mode)
{
case Mode.BreadthFirstSearch:
ExpandFrontierBreadthFirst(currentNode);
break;
case Mode.Dijkstra:
ExpandFrontierDijkstra(currentNode);
break;
case Mode.GreedyBestFirst:
ExpandFrontierGreedyBestFirst(currentNode);
break;
case Mode.AStar:
ExpandFrontierAStar(currentNode);
break;
default:
break;
}
// if the goal node is in the frontier
if (m_frontierNodes.Contains(m_goalNode))
{
// set the path Nodes
m_pathNodes = GetPathNodes(m_goalNode);
// if exitOnGoal is checked, mark the search complete
if (exitOnGoal)
{
isComplete = true;
}
}
}
// ...else we have explored the entire available graph
else
{
isComplete = true;
}
}
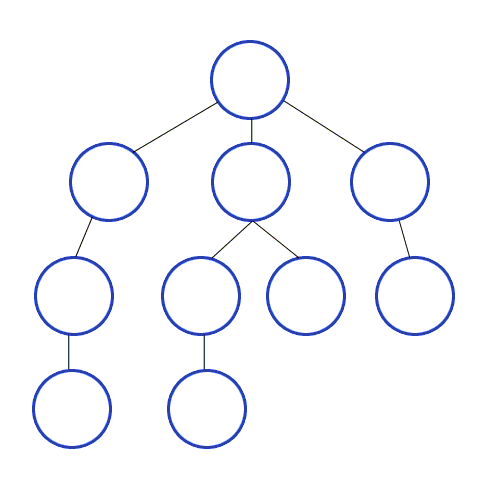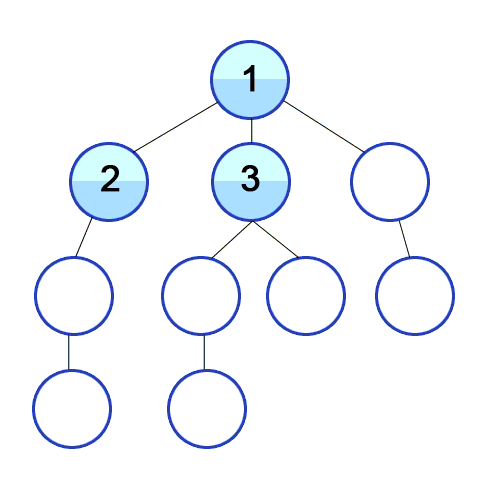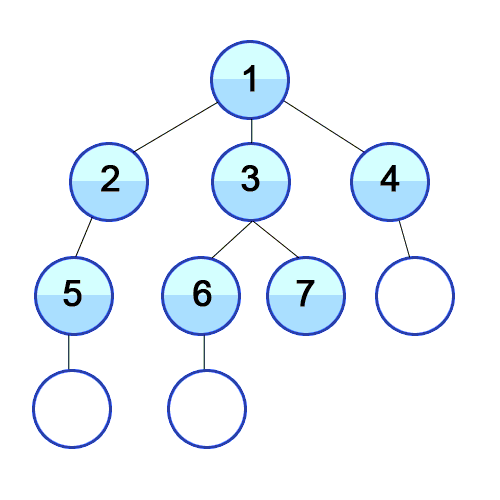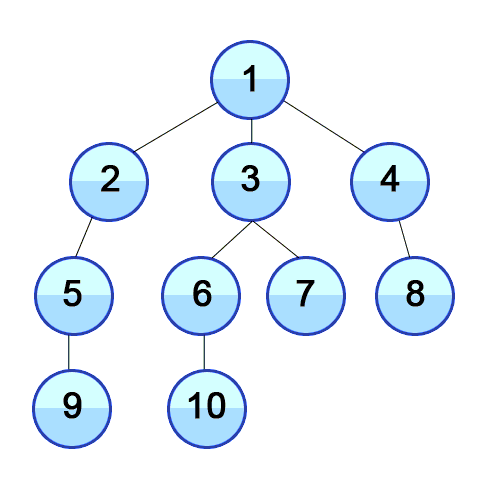
This most basic pathfinding algorithm is Breadth-first search (BFS), which is an algorithm for traversing or searching tree or graph data structures. It starts at the tree root (or some arbitrary node of a graph, sometimes referred to as a ‘search key’) and explores the neighbor nodes first, before moving to the next level neighbours.
// Expand the frontier nodes using Breadth First Search from a single node
void ExpandFrontierBreadthFirst(Node node)
{
if (node != null)
{
// Loop through the neighbors
for (int i = 0; i < node.neighbors.Count; i++)
{
// If the current neighbor has not been explored and is not already part of the frontier
if (!m_exploredNodes.Contains(node.neighbors[i]) && !m_frontierNodes.Contains(node.neighbors[i]))
{
// Calculate distance to current neighbor
float distanceToNeighbor = m_graph.GetNodeDistance(node, node.neighbors[i]);
// Calculate cumulative distance if we travel to neighbor via the current node
float newDistanceTraveled = distanceToNeighbor + node.distanceTraveled + (int)node.nodeType;
// Create breadcrumb trail to neighbor node and set cumulative distance traveled
node.neighbors[i].distanceTraveled = newDistanceTraveled;
node.neighbors[i].previous = node;
// Add neighbor to explored Nodes, treat queue as if it were a first in-first out queue
node.neighbors[i].priority = m_exploredNodes.Count;
m_frontierNodes.Enqueue(node.neighbors[i]);
}
}
}
}
Dijkstra Algorithm is the improvement of BFS, because BFS doesn’t really find the shortest path. So what do we need to change:
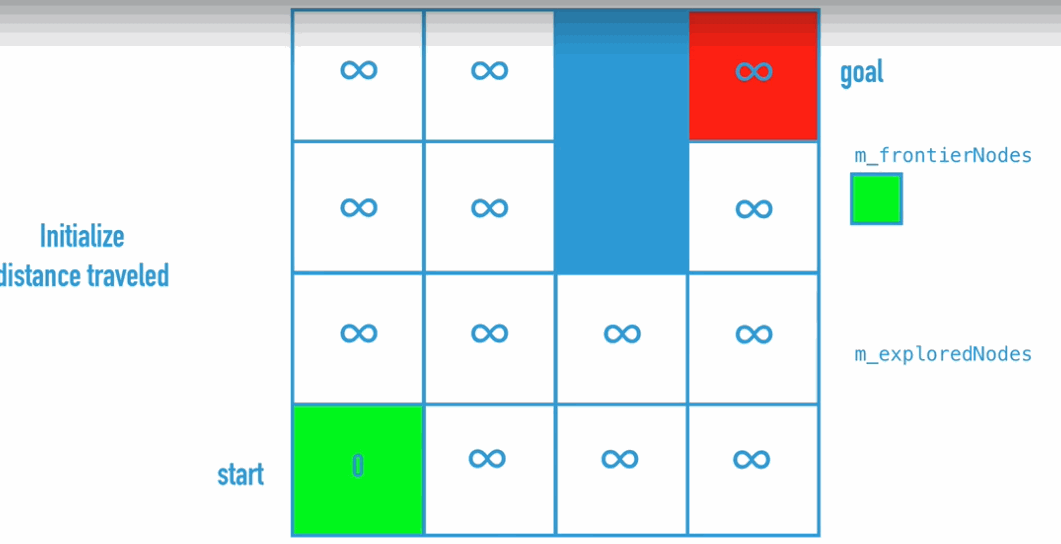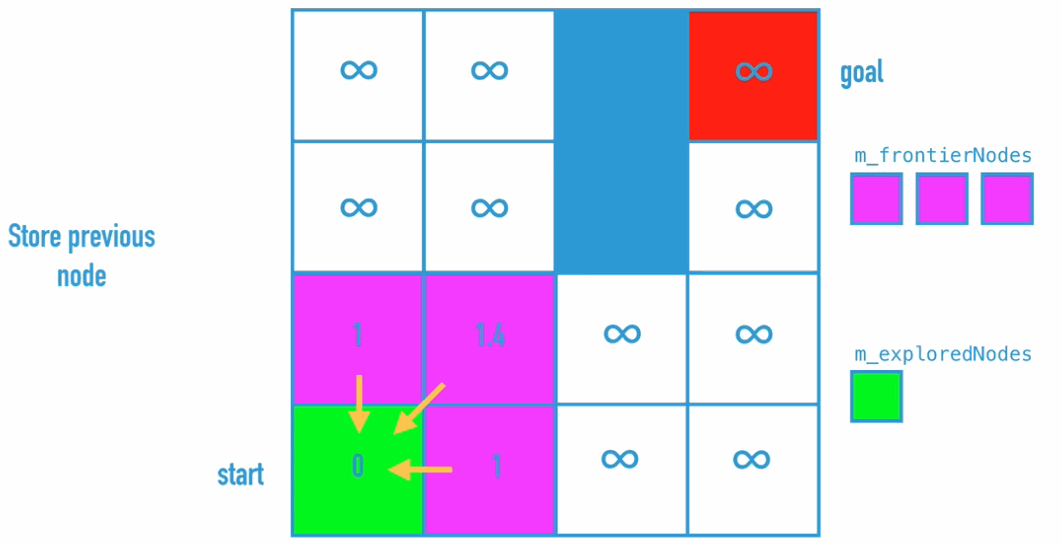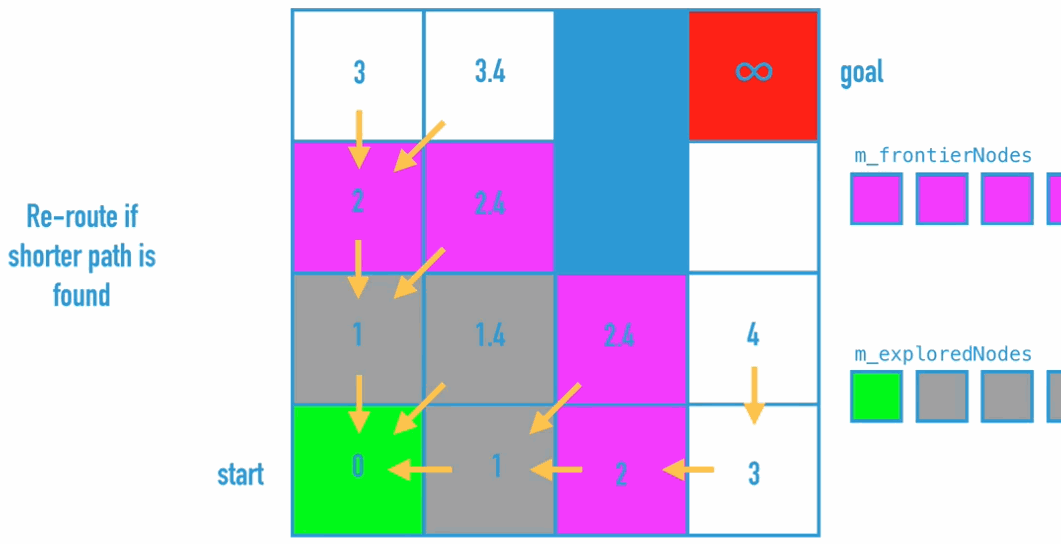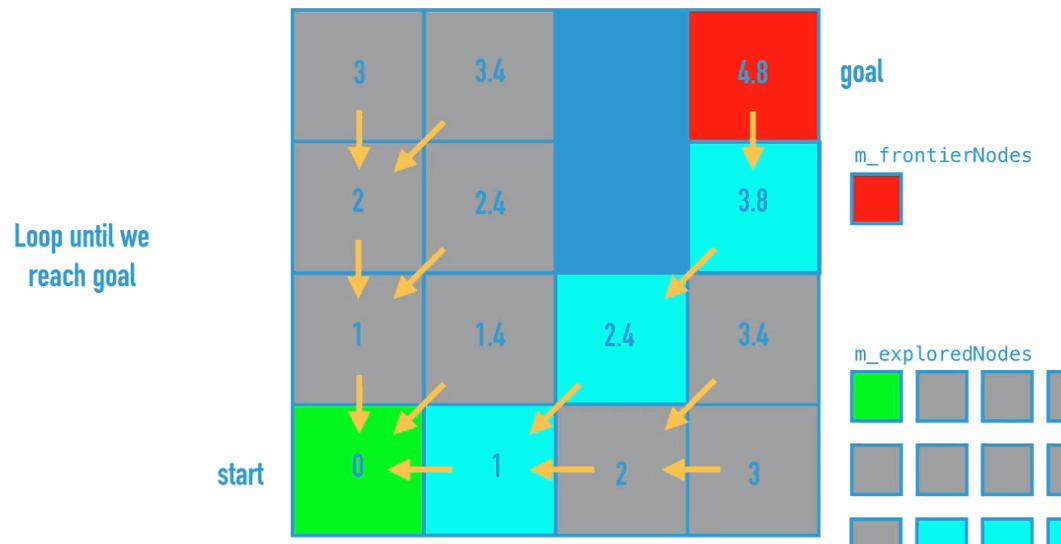
Code Implementation:
// expand the frontier nodes using Dijkstra's algorithm from a single node
void ExpandFrontierDijkstra(Node node)
{
if (node != null)
{
// loop through the neighbors
for (int i = 0; i < node.neighbors.Count; i++)
{
// if the current neighbor has not been explored
if (!m_exploredNodes.Contains(node.neighbors[i]))
{
float distanceToNeighbor = m_graph.GetNodeDistance(node, node.neighbors[i]);
float newDistanceTraveled = distanceToNeighbor + node.distanceTraveled + (int)node.nodeType;
// if a shorter path exists to the neighbor via this node, re-route
if (float.IsPositiveInfinity(node.neighbors[i].distanceTraveled) || newDistanceTraveled < node.neighbors[i].distanceTraveled)
{
node.neighbors[i].previous = node;
node.neighbors[i].distanceTraveled = newDistanceTraveled;
}
// if the current neighbor is not already part of the frontier...
if (!m_frontierNodes.Contains(node.neighbors[i]))
{
// set the priority based on distance traveled from start Node and add to frontier
node.neighbors[i].priority = node.neighbors[i].distanceTraveled;
m_frontierNodes.Enqueue(node.neighbors[i]);
}
}
}
}
}
Greedy Best-First Search are always looking for the shortest distance between start and goal node. Therefore it is often not the shortest path even worse than BFS, but it is the fastest way to find the goal.
The algorithm works as follows:
- Start by putting any one of the graph’s vertices at the back of a queue.
- Take the front item of the queue and add it to the visited list.
- Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the back of the queue.
- Keep repeating steps 2 and 3 until the queue is empty.

// expand the frontier nodes using Greedy Best-First search from a single node
void ExpandFrontierGreedyBestFirst(Node node)
{
if (node != null)
{
// loop through the neighbors
for (int i = 0; i < node.neighbors.Count; i++)
{
// if the current neighbor has not been explored and is not already part of the frontier
if (!m_exploredNodes.Contains(node.neighbors[i]) && !m_frontierNodes.Contains(node.neighbors[i]))
{
// calculate distance to current neighbor
float distanceToNeighbor = m_graph.GetNodeDistance(node, node.neighbors[i]);
// calculate cumulative distance if we travel to neighbor via the current node
float newDistanceTraveled = distanceToNeighbor + node.distanceTraveled + (int)node.nodeType;
// create breadcrumb trail to neighbor node and set cumulative distance traveled
node.neighbors[i].distanceTraveled = newDistanceTraveled;
node.neighbors[i].previous = node;
// set the priority based on estimated distance to goal Node...
if (m_graph != null)
{
node.neighbors[i].priority = m_graph.GetNodeDistance( node.neighbors[i], m_goalNode);
}
// ... and add to frontier
m_frontierNodes.Enqueue(node.neighbors[i]);
}
}
}
}
A* algorithm is actually a combination of Dijkstra Algorithm and Greedy Best-First Search Algorithm. For example, in Dijkstra algorithm, it calculates the distance from current node to start node. In the Greedy Best-First Search, it is to calculate the distance from current node to target node. A* algorithm is a combination of these two algorithms to get the best priority: * Distance from current node to start node = G * Distance from current node to target node = H * A*: F = G+H

// expand the frontier nodes using AStar search from a single node
void ExpandFrontierAStar(Node node)
{
if (node != null)
{
// loop through the neighbors
for (int i = 0; i < node.neighbors.Count; i++)
{
// if the current neighbor has not been explored...
if (!m_exploredNodes.Contains(node.neighbors[i]))
{
// calculate distance to current neighbor
float distanceToNeighbor = m_graph.GetNodeDistance(node, node.neighbors[i]);
// calculate cumulative distance if we travel to neighbor via the current node
float newDistanceTraveled = distanceToNeighbor + node.distanceTraveled + (int)node.nodeType;
// if a shorter path exists to the neighbor via this node, re-route
if (float.IsPositiveInfinity(node.neighbors[i].distanceTraveled) || newDistanceTraveled < node.neighbors[i].distanceTraveled)
{
node.neighbors[i].previous = node;
node.neighbors[i].distanceTraveled = newDistanceTraveled;
}
// if the neighbor is not part of the frontier, add this to the priority queue
if (!m_frontierNodes.Contains(node.neighbors[i]) && m_graph != null)
{
// base priority, F score, on G score (distance from start) + H score (estimated distance to goal)
float distanceToGoal = m_graph.GetNodeDistance(node.neighbors[i], m_goalNode);
node.neighbors[i].priority = node.neighbors[i].distanceTraveled + distanceToGoal;
// add to priority queue using the F score
m_frontierNodes.Enqueue(node.neighbors[i]);
}
}
}
}
}
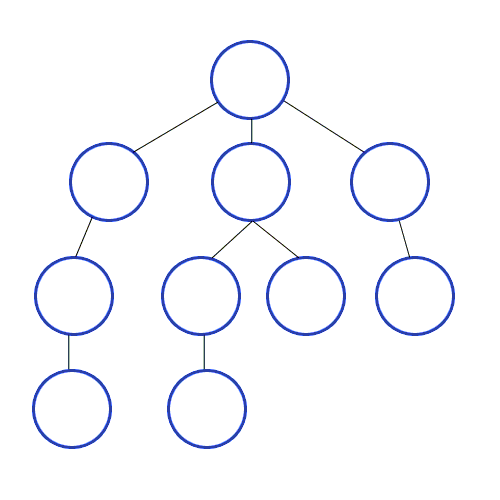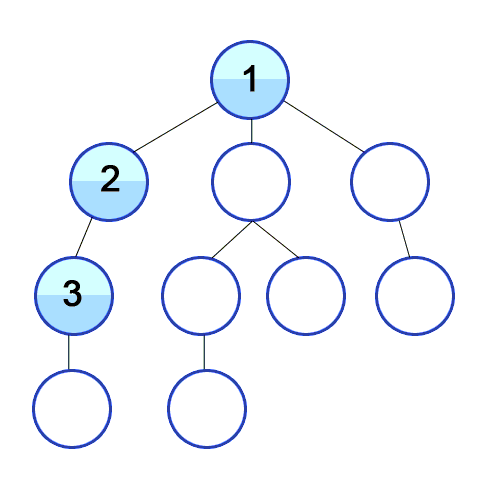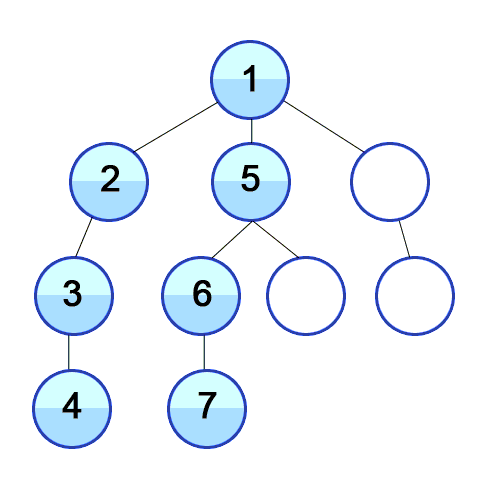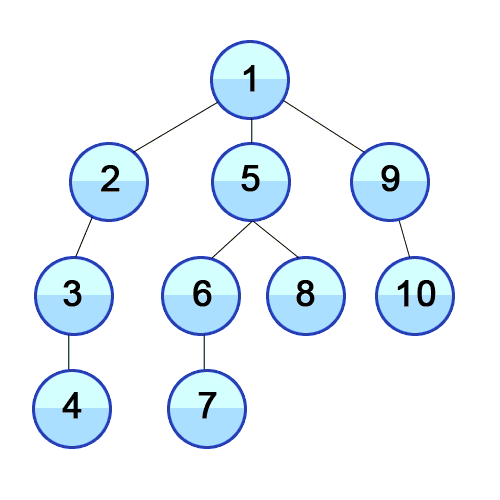
Depth-First Search is a recursive algorithm for searching all the vertices of a graph or tree data. structure.
The algorithm works as follows:
- Start by putting any one of the graph’s vertices at the back of a queue.
- Take the front item of the queue and add it to the visited list.
- Create a list of that vertex’s adjacent nodes. Add the ones which aren’t in the visited list to the back of the queue.
- Keep repeating steps 2 and 3 until the queue is empty.
public HashSet<T> DFS<T>(Graph<T> graph, T start)
{
var visited = new HashSet<T>();
if (!graph.AdjacencyList.ContainsKey(start))
return visited;
var stack = new Stack<T>();
stack.Push(start);
while (stack.Count > 0)
{
var vertex = stack.Pop();
if (visited.Contains(vertex))
continue;
visited.Add(vertex);
foreach (var neighbor in graph.AdjacencyList[vertex])
if (!visited.Contains(neighbor))
stack.Push(neighbor);
}
return visited;
}
End –Cheng Gu