3 Aug 2018

Partial Derivative in Shader

Currently found a post talked about ddx, and ddy function in shader, so here is a conclusion from that post, and some examples.

This is the Reference Link

Partial Derivative(ddx,ddy)

In Shader Language, The partial derivative functions are divided into HLSL: ddx and ddy; GLSL:dFdx and dFdy, respectively corresponding to the change rate of various variables in the pixel block in the screen space on the x and y axes.

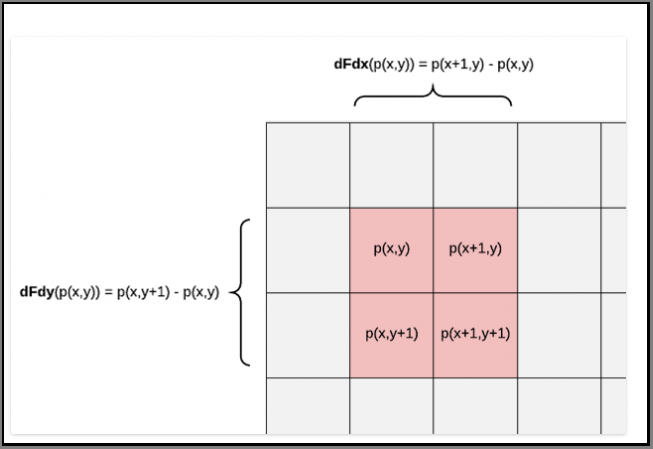
This image illustrates the calculation of Partial Derivative.

As We know, during the Rasterization, GPUs will run many Fragment shaders in parallel at the same time, but it is not performed pixel by pixel, but by organizing them into a group of pixels at 2x2 pixels to execute in parallel. And the partial derivative is exactly the rate of change in this pixel. It can be seen from the figure above that ddx() is the value of the pixel block on the right minus the value of the pixel block on the left, while ddy is the value of the pixel block below minus the value of the pixel block above. Where x and y represent screen coordinates.

Notices: Partial derivative ddx / ddy can calculate any variable in Fragment Shader. such as Vectors, matrices and so on.

Example 1: Derivatives and mipmaps (For UV)

In 3D world, the size of image is related to the location of the camera. When it is close to the camera, the actual pixel of the picture is bigger; when it is far away from the camera, the actual pixel of the picture is smaller. For example, a 64x64 image may show 5050 pixels when it is close to the camera; when it is far away, it may only show 2020 pixels. So, if the texture pixel is always the orginal number, when it is far away from the camera, this will lead to performance waste.

Mipmap texture Technology is currnetly the most effective way to solve the relationship between texture resolution and the distance between view points. it will first compress images into many progressively smaller images.

“Derivatives are used during texture sampling to select the best mipmap level. The rate of variation of the texture coordinates with respect to the screen coordinates is used to choose a mipmap; the larger the derivatives, the greater the mipmap level (and the lesser the mipmap size).”

Example 2: Face normal computation / Flat Shader(For vertex)

Derivatives can be used to compute the current triangle’s face normal in a fragment shader. The horizontal and vertical derivatives of the current fragment’s world-position are two vectors laying in the triangle’s surface. Their cross product is a vector orthogonal to the surface and its norm is the triangle’s normal vector (see the 3d model below).

Particular attention must be paid to the ordering of the cross product: being the OpenGL coordinate system left-handed (at least when working in window space which is the context where the fragment shader works) and being the horizontal derivative vector always oriented right and the vertical down, the ordering of the cross product to obtain a normal vector oriented toward the camera is horizontal x vertical (more about cross products and basis orientations in this article).

The interactive model below shows the link between screen pixels and fragmets over a triangle surface being rasterized, the derivative vectors on the surface (in red and green), and the normal vector (in blue) obtained by the cross product of the twos.

The normal is shown in Unity shaderlab as follows

void surf (Input IN, inout SurfaceOutput o)
{
    o.Albedo = normalize(cross(ddy(IN.worldPos),ddx(IN.worldPos)));
}

Example 3: Sharpen Edge (For Texture)

void surf (Input IN, inout SurfaceOutput o)
{
    half4 c = tex2D(_MainTex, IN.uv_MainTex);
    
    //The comparsion is depends on this
    //c += ddx(c)*2 + ddy(c)*2; 
    o.Albedo = c.rgb;
    o.Alpha = c.a;
}

Example 4: Blur image except the pixels which are facing towards camera

Shader "MyShader/SimpleBlur"
{
	Properties
	{
		_MainTex ("Texture", 2D) = "white" {}
	}
	SubShader
	{
		Tags { "RenderType"="Opaque" }

		Pass
		{
			CGPROGRAM
			#pragma vertex vert
			#pragma fragment frag

			#include "UnityCG.cginc"

			struct appdata
			{
				float4 vertex : POSITION;
				float2 texcoord : TEXCOORD0;
			};

			struct v2f
			{
                float4 pos : SV_POSITION;
				float2 uv : TEXCOORD0;
                float z : TEXCOORD1;
			};

			sampler2D _MainTex;
			
			v2f vert (appdata v)
			{
				v2f o;
				o.pos = UnityObjectToClipPos(v.vertex);
                
                o.uv = v.texcoord.xy;
                o.z = mul(unity_ObjectToWorld, v.vertex).z;
				return o;
			}
			
			fixed4 frag (v2f i) : SV_Target
			{
                float2 dsdx = ddx(i.z)*10;
                float2 dsdy = ddy(i.z)*10;

				fixed4 col = tex2D(_MainTex, i.uv, dsdx, dsdy);

				return col;
			}
			ENDCG
		}
	}
}